Stability of Legged Robots
#Robotics #Modeling For controlled nonlinear dynamical systems, there are a number of useful concepts relating to their safety and stability, including:
- Fixed points: Stable fixed points represent the static postures in which the robot can safely stand still.
- Limit cycles: Limit cycles provide a natural extension of fixed-point analysis to periodic walking or running motions.
- Viability: Viability is a concept of controlled invariance, which analyzes the set of states from which the robot is able to avoid to fall.
- Controllability: Controllability provides a slightly restricted notion of viability, analyzing the set of states from which the robot is capable of returning to a particular fixed point (or limit cycle).
In addition, useful tools are available to analyze the stability of a legged robot in presence of disturbances or modeling uncertainties. Some of these tools are:
- Robust stability: Robust stability (or viability) examines the properties of the system considering worst-case (bounded) disturbances. For instance, a robust controller may be able to guarantee that a fixed point is stable even if the estimate of the mass of the trunk is wrong by $\pm10$ %.
- Stochastic stability: Stochastic analysis provides tools to investigate the probability of falling down.
- Input-output stability: This analysis treats a particular disturbance as an input, a performance criteria as output, and attempts to compute a relative gain or sensitivity of the robot performance due to this input.
- Stability margins: Robustness analysis can be difficult. In practice control designers often settle for the system staying comfortably away from the boundaries of deterministic stability.
Each of the above will be explained thoroughly below.
Fixed Points
Fixed point in the context of robotics apparently refers to equilibrium points. For a system with dynamics $\dot{x} = f(x)$, a point $x^\ast$ is called a fixed point if $f(x^\ast) = 0$. For the model of a legged robot that we have in this note, a fixed point is a configuration $q^\ast$ for which $\dot{q^\ast} = 0$ and $\ddot{q^\ast} = 0$ is a solution to the equation. For a fixed point we’ll then have $\ddot{c} = 0$ and $\dot{L}$ = 0 which in turn gives
\(c^{x, y} - \frac{c^z}{g^z} g^{x, y}= z^{x, y} \in \text{conv}\ {p_i^{x, y}}\)
This necessary condition states that the CoM, $c$, must project on the ground along the gravity vector, $−g$, inside the convex hull of the contact points, $p_i$, also known as the support polygon.
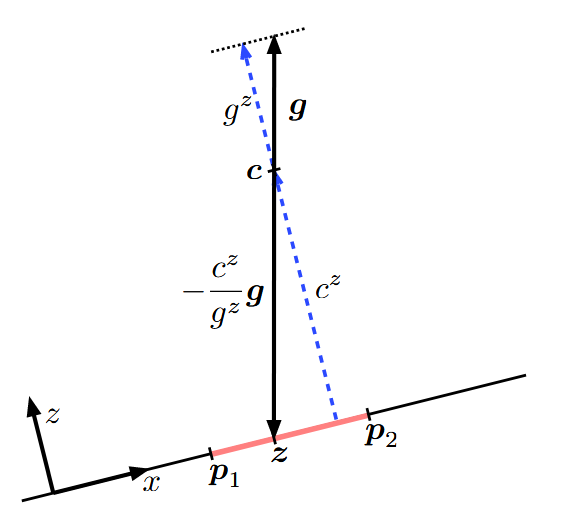The stability of fixed points can be analyzed, perhaps by linearizing the dynamics at the fixed point and using linear system analysis tools. Indeed, these tools can also be applied here, under the strong assumption that the contact conditions do not change (e.g., either $f_i^z = 0$ and $p_i^z \geq 0$, or $f_i^z \geq 0$ and $p_i^z = 0$).
Limit Cycles
a
Sources: